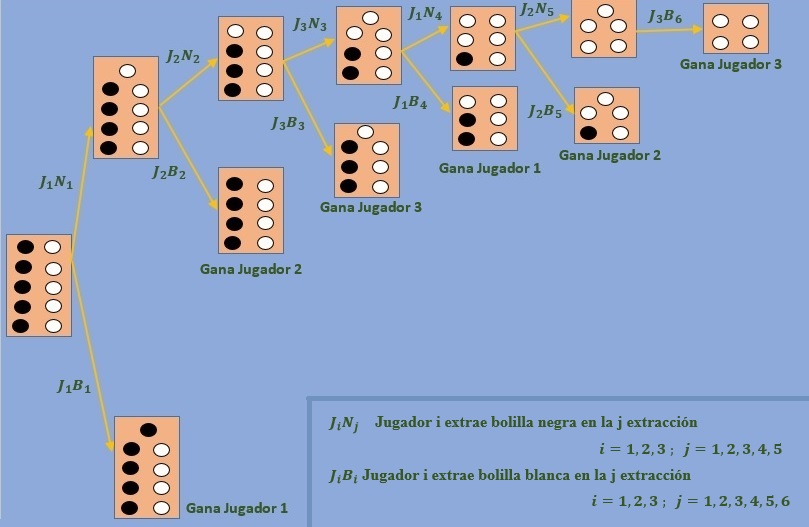
Problema: Tres jugadores van sacando alternadamente y sin reponerla una bolilla de una urna que contiene 5 blancas y 5 negras. Gana el juego el que saca la primera bolilla blanca. ¿Cuál es la probabilidad de ganar que tiene cada jugador?.

Desarrollo

El la grafica anterior se presenta las distintas alternativas que podrian suceder en las extracciones de las bolillas, tanto para el jugador 1, 2 y 3.

Se puede notar que no hay una independencia en las extracciones, por lo que se tiene que al aplicar la probabilidad condicional:

 Es decir la probabilidad de que el jugador 1 saque una bolilla blanca en la primera extracion es 0,5 y que sea blanca en la cuarta extraccion es 0,06 por lo que la probabilidad de ganar que tiene el jugador 1 es la suma de 0,5 con 0,06 teniendo así una valor correspondiente a 0,56.

Procedemos de igual forma para el jugador 2 y 3

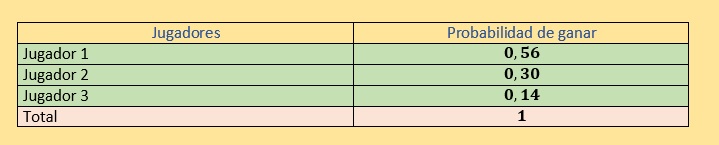
Podemos observar en la siguiente tabla las probabilidades de ganar que tiene cada jugador. Se puede ver que el jugador 1 tiene altas chances de ganar, siguiendole el jugador 2 y por ultimo el jugador 3.

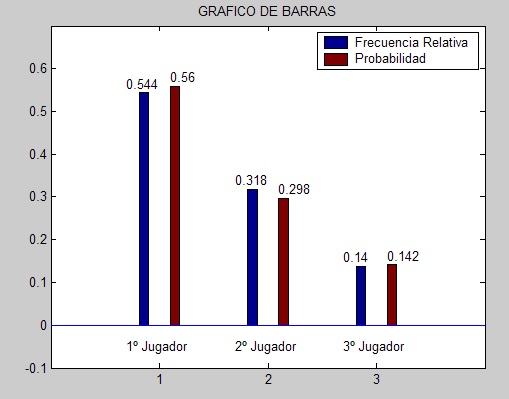
A continuacion presentamos las pantallas de un simulación del problema realizado con el software Matlab, donde se trabajara con dos muestras, una muestra de cantidad 500 y la otra de 5000.

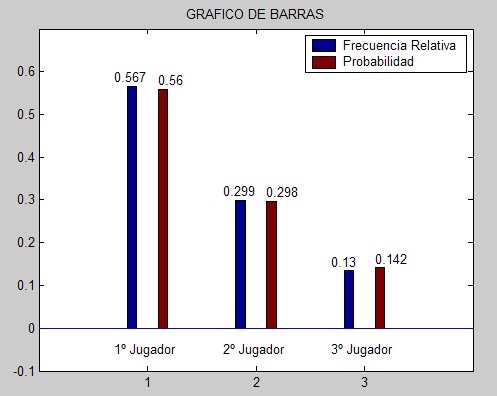
Ahora se mostrara la misma simulación pero con una muestra de tamaño 5000.

Cuando realizamos el lanzamiento de un dado perfecto los valores posibles a obtener por el tirador son el 1,2,..,6 en donde la probabilidad que corresponde a cada valor es 1/6. Pero que si en vez de lanzar un dado queremos lanzar dos dados perfectos a la vez y sumar sus puntos ( o lanzar un dado dos veces y sumar sus puntos). Para ello proponemos el siguiente desarrollo:

Los valores que podemos tomar en cada lanzamiento son lo siguientes, 2,3,4,5,..,12 es decir la suma de los puntos de los dados a dichos valores los representaremos con la variable aleatoria X. Suponiendo que realizamos un cierto numero de lanzamientos n, es decir por cada suma de puntos podemos saber las veces que se dio “esa suma” en los n lanzamiento, esto no es nada mas que la frecuencia absoluta de la variable X. Conociendo la frecuencia absoluta podemos obtener la frecuencia relativa, la cual se encuentra para cada valor de la variable X, dividiendo en numero de observaciones por el total de lanzamientos.

La probabilidad de cada valor de variable se obtiene a partir de la definición clasica de Laplace en donde: La probabilidad de un suceso es el cociente del numero de caso favorables por el numero de casos posbles

P(X) = c/n

Podemos observarlo de mejor manero en nuestro espacio muestral

Casa caso representa una tupla en donde el primer valor corresponde a los puntos del primer dado y el segundo a los del segundo dado.

A continuación presentamos en geogebra la simulación de los lanzamientos de los dados, en esta simulación realizaremos 3000 lanzamientos