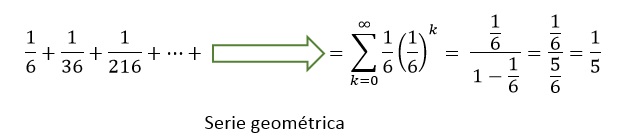
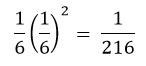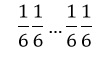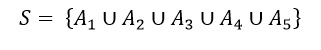Problema: De una urna con a bolas azules y b blancas se extrae una al azar y se la repone agregando además c bolas de mismo color que la extraída. Luego se repite el procedimiento. ¿Cuál es la probabilidad de sacar bolas azules en las dos primeras extracciones? ¿y de que sean azules las tres primeras?

Desarrollo

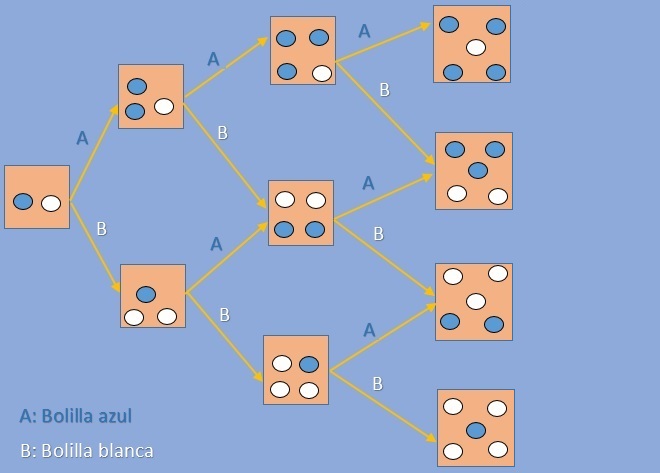
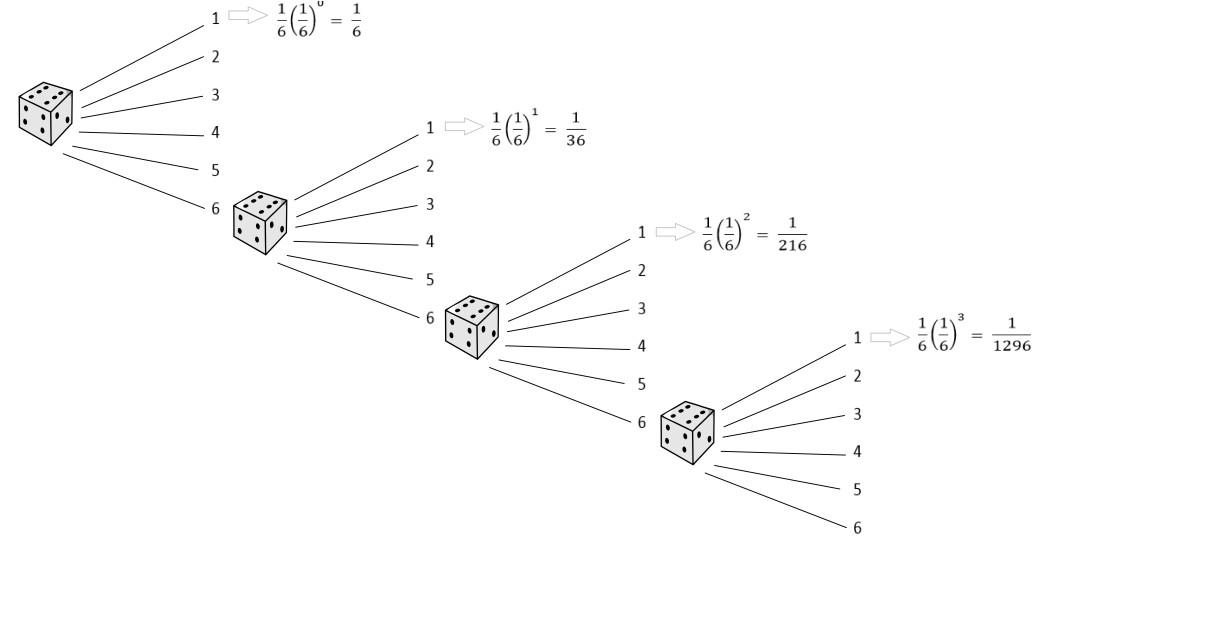
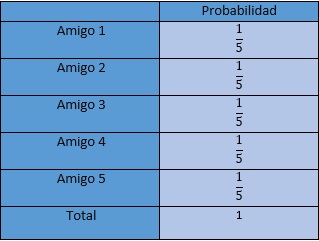
A continuacion presentamos una grafica para entender mejor el problema, con el caso especial en que la urna comiece con una bola azul y una blanca y se agrega una de mismo color

Sucesos:

A: Bola Azul

B: Bola Blanca

A continuación mostraremos el caso base mostrado en el gráfico, en donde a=b=c=1

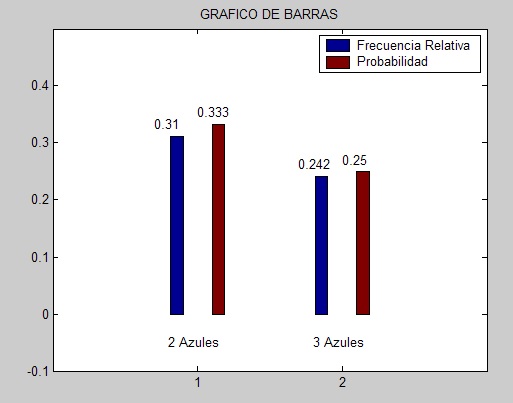
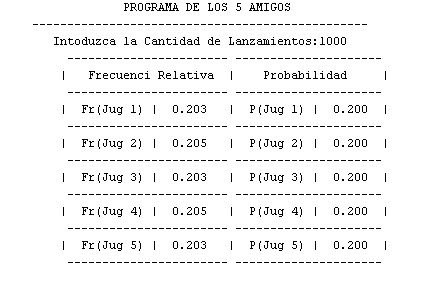
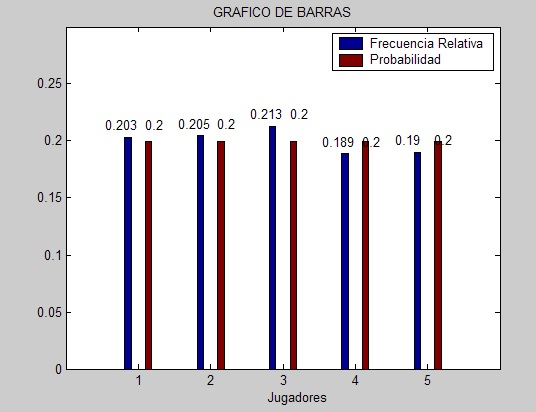
Para verificarlo, procedemos a simularlo, tomamos a este caso como el “caso base” donde a=b=c=1 con una muestra de 500:

Vemos que la probabilidad de sacar dos azules en la segunda extracción es 0.33 y que su frecuencia esta muy proxima, 0.31. En el caso de que sean azules en la tercera extracción, su probabilidad es 0.25 y su frecuencia 0.242.

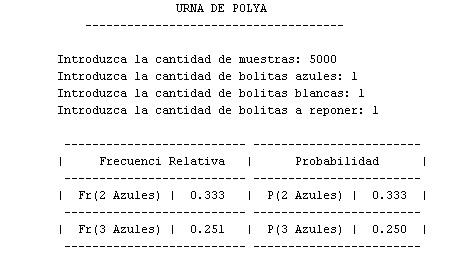
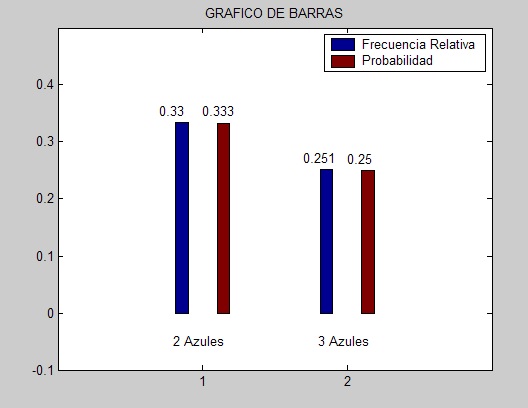
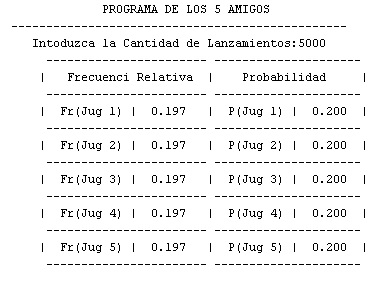
   Repetimos la simulacion del caso base, pero ahora con una muestra de 5000:

Se puede observar claramente que al incrementar el tamaño de la muestra, hay una gran aproximacion.

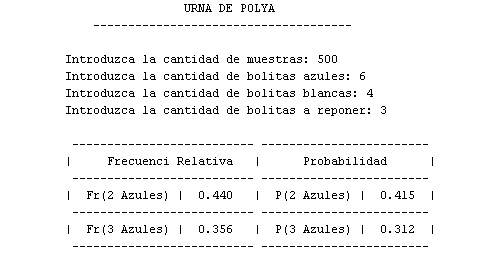
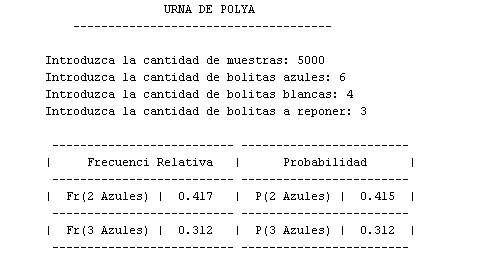
   Como los requerimientos del problema son que tenemos “a” bolas azules, “b” bolas blancas y “c” bolas se reponen. Estos requerimientos son solicitados por el software. Como ser un “caso variado” en que haya 6 bolas azules, 4 blancas y que reposición 3 en una muestra de 500.

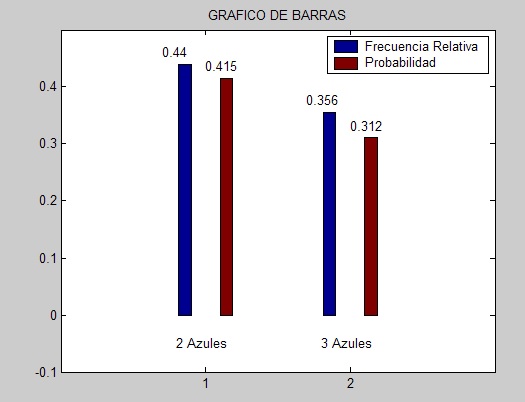
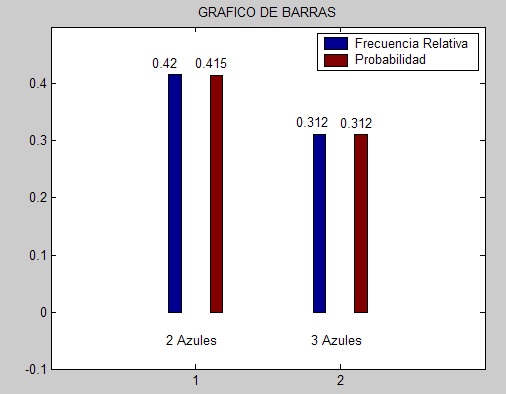
al igual que en el caso base (con una muestra de 500) hay poca aproximacion de la frecuencia con la probabilidad. Pero incrementado el tamaño de muestra a 5000 (en el caso variado), vemos que:

El software cumple con los requerimientos del problema para cualquier a,b,c > 0

Problema: En cierta ocacion un grupo de 5 estudiantes de probabilidades se junto a almorzar en el bar de la facultad. Llegada la hora de obonar la factura, a uno de ello se le ocurrio la idea de sortear quien pagaria la cuenta. Para ello estrajo un dado perfecto de 6 caras, proponiedo la siguiente regla:

A cada estudiente asignarle un numero del dado, es decir, al primer estudiante el numero 1, al segundo el 2 y asi suscesivemente hasta el quinto estudiante. En cambio la cara 6 del dado corresponde a un nuevo lanzamiento del dado.

Pero los amigos dudan de que todos tengan la misma probabilidad de ocurrencia de ser elegidos al lanzar el dado.

¿Como hace el alumno que propone el sorteo con el dado para fundamentar su propuesta?

Desarrollo

Supongamos que un alumno (o otra persona) arroja el dado y sale el “1” en ese caso el alumno UNO paga la cuenta, pero si sale el “6” se lanzará nuevamente el dado, por lo que podemos representarlo mediante la siguiente grafica.

Casos favorables al “1”

La probabilidad de que salga el “1” es:

La probabilidad de que salga el “1” dado que anteriormete salio el “6” , es decir, se lanzo nuevamente el dado es:

 

 

La probabilidad de que salga el “1” dado que anteriormete salio el “6”  dos veces consecutivas,  es:

 

 

La probabilidad de que salga el “1” dado que anteriormete salio el “6”  n veces consecutivas,  es:

 

 

Entonces teniendo en cuenta a todos los casos favorables a que salga el 1 en el ultima lanzamiento, la probabilidad de que el jugador 1 pague la cuenta es la sumatoria de todas las probabilidades de estos casos, es decir:

Por lo que la probabilidad de que salga el “1”  (paga la cuenta el amigo “1”) es 1/5.  Analogamente procedemos para los subconjuntos que se muestran a continuacion, donde obtendremos las probabilidades para el amigo 2,3,4 y 5 respectivamente. Notaremos que para el amigo 2,3,4, y 5 obtenemos una probabilidad igual a 1/5 para cada uno

Por lo que el espacio muestral final sera la union de cada uno de los espacios favorables al 1 al 2, 3,4, y 5

 Conclusión

El metodo propuesto por el amigo “1” equivale a tener un experimento con igual probabilidad de ser elegidos cada uno de los amigos para pagar la cena y dicha probabilidad es 1/5 para cada uno de los amigos.

 A continuacion presentamos las pantallas de un simulación del problema realizado con el software Matlab, donde se trabajara con dos muestras, una muestra de cantidad 1000 y la otra de 5000.

Muestra de 1000

Muestra de 5000