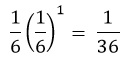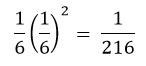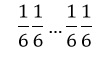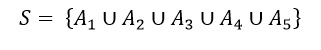Problema: En cierta ocacion un grupo de 5 estudiantes de probabilidades se junto a almorzar en el bar de la facultad. Llegada la hora de obonar la factura, a uno de ello se le ocurrio la idea de sortear quien pagaria la cuenta. Para ello estrajo un dado perfecto de 6 caras, proponiedo la siguiente regla:
A cada estudiente asignarle un numero del dado, es decir, al primer estudiante el numero 1, al segundo el 2 y asi suscesivemente hasta el quinto estudiante. En cambio la cara 6 del dado corresponde a un nuevo lanzamiento del dado.
Pero los amigos dudan de que todos tengan la misma probabilidad de ocurrencia de ser elegidos al lanzar el dado.
¿Como hace el alumno que propone el sorteo con el dado para fundamentar su propuesta?
Desarrollo
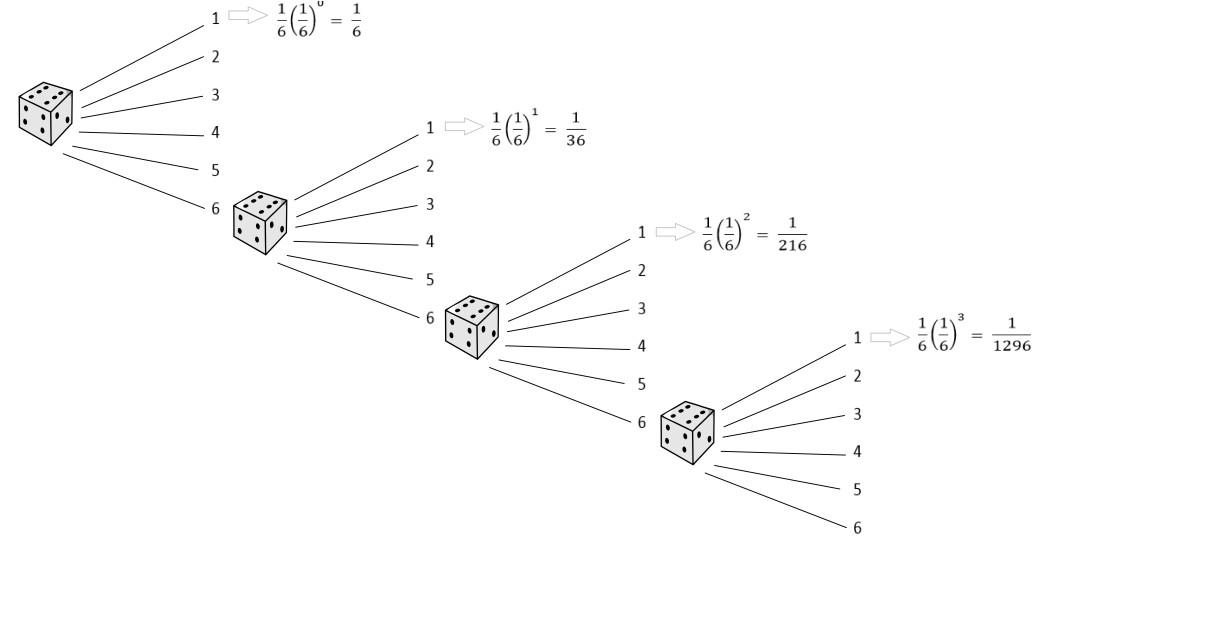
Supongamos que un alumno (o otra persona) arroja el dado y sale el “1” en ese caso el alumno UNO paga la cuenta, pero si sale el “6” se lanzará nuevamente el dado, por lo que podemos representarlo mediante la siguiente grafica.
Casos favorables al “1”
![]() La probabilidad de que salga el “1” es:
La probabilidad de que salga el “1” es:
La probabilidad de que salga el “1” dado que anteriormete salio el “6” , es decir, se lanzo nuevamente el dado es:
La probabilidad de que salga el “1” dado que anteriormete salio el “6” dos veces consecutivas, es:
La probabilidad de que salga el “1” dado que anteriormete salio el “6” n veces consecutivas, es:
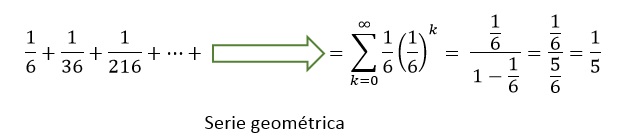
Entonces teniendo en cuenta a todos los casos favorables a que salga el 1 en el ultima lanzamiento, la probabilidad de que el jugador 1 pague la cuenta es la sumatoria de todas las probabilidades de estos casos, es decir:
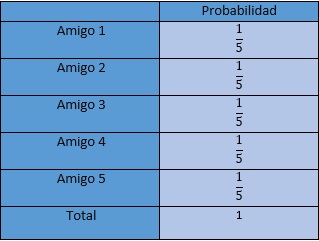
Por lo que la probabilidad de que salga el “1” (paga la cuenta el amigo “1”) es 1/5. Analogamente procedemos para los subconjuntos que se muestran a continuacion, donde obtendremos las probabilidades para el amigo 2,3,4 y 5 respectivamente. Notaremos que para el amigo 2,3,4, y 5 obtenemos una probabilidad igual a 1/5 para cada uno
Por lo que el espacio muestral final sera la union de cada uno de los espacios favorables al 1 al 2, 3,4, y 5
Conclusión
El metodo propuesto por el amigo “1” equivale a tener un experimento con igual probabilidad de ser elegidos cada uno de los amigos para pagar la cena y dicha probabilidad es 1/5 para cada uno de los amigos.
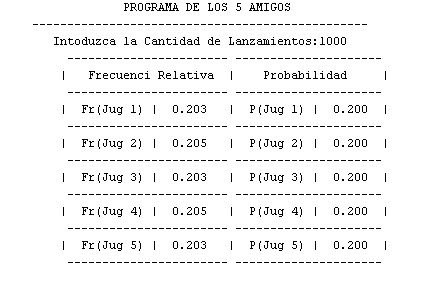
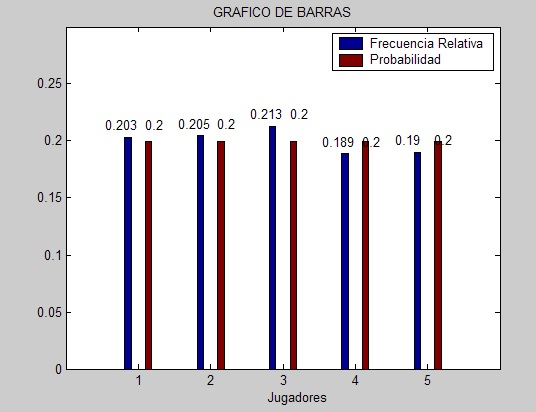
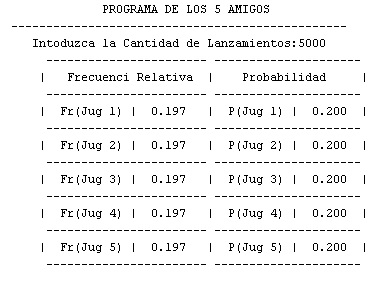
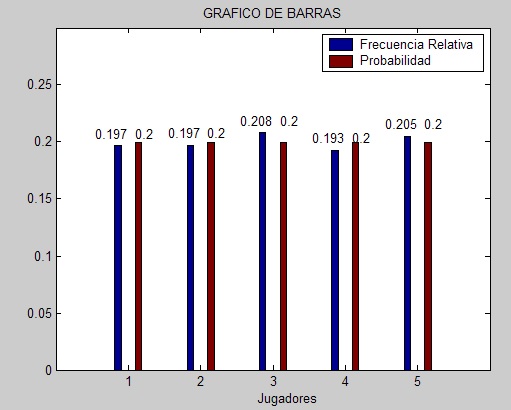
A continuacion presentamos las pantallas de un simulación del problema realizado con el software Matlab, donde se trabajara con dos muestras, una muestra de cantidad 1000 y la otra de 5000.
Muestra de 1000
Muestra de 5000